In a previous post I provided an introduction to the generic heap data structure and how it's used by the .NET PriorityQueue type. In the subsequent post I discussed the implementation of some important methods on PriorityQueue. In this post, we look at the Remove() method, which was added in .NET 9 (preview 1), and show how you can use it to implement Dijkstra's algorithm for finding the shortest path between two nodes.
The rationale for adding PriorityQueue.Remove()
The PriorityQueue type introduced in .NET 6 supports most of the common operations you'd expect from a priority queue, with one main exception: priority updates. A priority update is where you change the priority of an already-enqueued node. While not essential, priority updates are important for some algorithms.
Whether or not to support priority updates was discussed in the original proposal, but ultimately it was decided not to include them as it would decrease overall performance. There is still a proposal for creating a new type that supports priority updates, but it looks unlikely to be implemented at this stage.
One such algorithm that requires priority updates is Dijkstra's algorithm. Dijkstra's algorithm is a popular, well-known, algorithm for finding the shortest path between two nodes. In its original form, this algorithm doesn't require a priority queue, but in practice, virtually all implementations use a priority queue.
While retrofitting priority updates to PriorityQueue was deemed not possible, a stop-gap approach was decided upon. Instead of enabling priority updates, a Remove() method was implemented, which allows updates.
This implementation might not be sufficient for all use cases, but it may be adequate for some. In particular, the original pull request calls out its use in leetCode challenges. It also points out that other languages, such as Java, have taken a similar approach with regard to priority updates.
In this post we'll take a brief look at the implementation of the Remove() method, then we'll look at how we can use it in an implementation of Dijkstra's algorithm.
The Remove() method in .NET 9 (preview 1)
The PriorityQueue.Remove() method takes an element TElement to search for, removes it from the heap, and returns it in out parameters. The annotated implementation below shows how it works:
public bool Remove(
TElement element, // The element to search for
[MaybeNullWhen(false)] out TElement removedElement, // When found, the element that was removed
[MaybeNullWhen(false)] out TPriority priority, // The priority of the element removed
IEqualityComparer<TElement>? equalityComparer = null) // The comparer to use to find the element
{
// Scans the heap for the first index that
// contains an element equal to the specified parameter.
int index = FindIndex(element, equalityComparer);
if (index < 0)
{
// the element wasn't found
removedElement = default;
priority = default;
return false;
}
// The element was found, so remove it from the heap
(TElement Element, TPriority Priority)[] nodes = _nodes;
(removedElement, priority) = nodes[index];
int newSize = --_size;
if (index < newSize)
{
// We're removing an element from the middle of the heap.
// Pop the last element in the collection "virtually" insert
// it in the hole from the removed node, and sift downward.
(TElement Element, TPriority Priority) lastNode = nodes[newSize];
if (_comparer == null)
{
MoveDownDefaultComparer(lastNode, index);
}
else
{
MoveDownCustomComparer(lastNode, index);
}
}
nodes[newSize] = default;
_version++;
return true;
}
The Remove method here first scans the whole heap to look for the element, which is an operation. As discussed in the previous post, MoveDownDefaultComparer has a similar complexity, so the overall complexity comes out to as well.
So how can you implement priority updates with the Remove() method? The solution is to combine Remove() with Enqueue(). For example:
var queue = new PriorityQueue<string, int>([
("A", 15),
("B", 7),
("C", 23),
("D", 27),
("E", 22),
]);
// update priority element "C" by removing and replacing
queue.Remove("C", out _, out _);
queue.Enqueue("C", "5");
queue.Peek(); // "C"
In the second half of this post, we'll look at how you can use this technique to implement Dijkstra's algorithm.
Implementing Dijkstra's algorithm
As mentioned previously, Dijkstra's algorithm is a well-known method for finding the shortest path between two nodes. In this post I'll show an implementation that uses .NET's PriorityQueue, including the new Remove() method.
A word of warning, I haven't tested this implementation in anything more than simple scenarios. The original implementation PR included a similar implementation, although that version is even more simplistic in many ways.
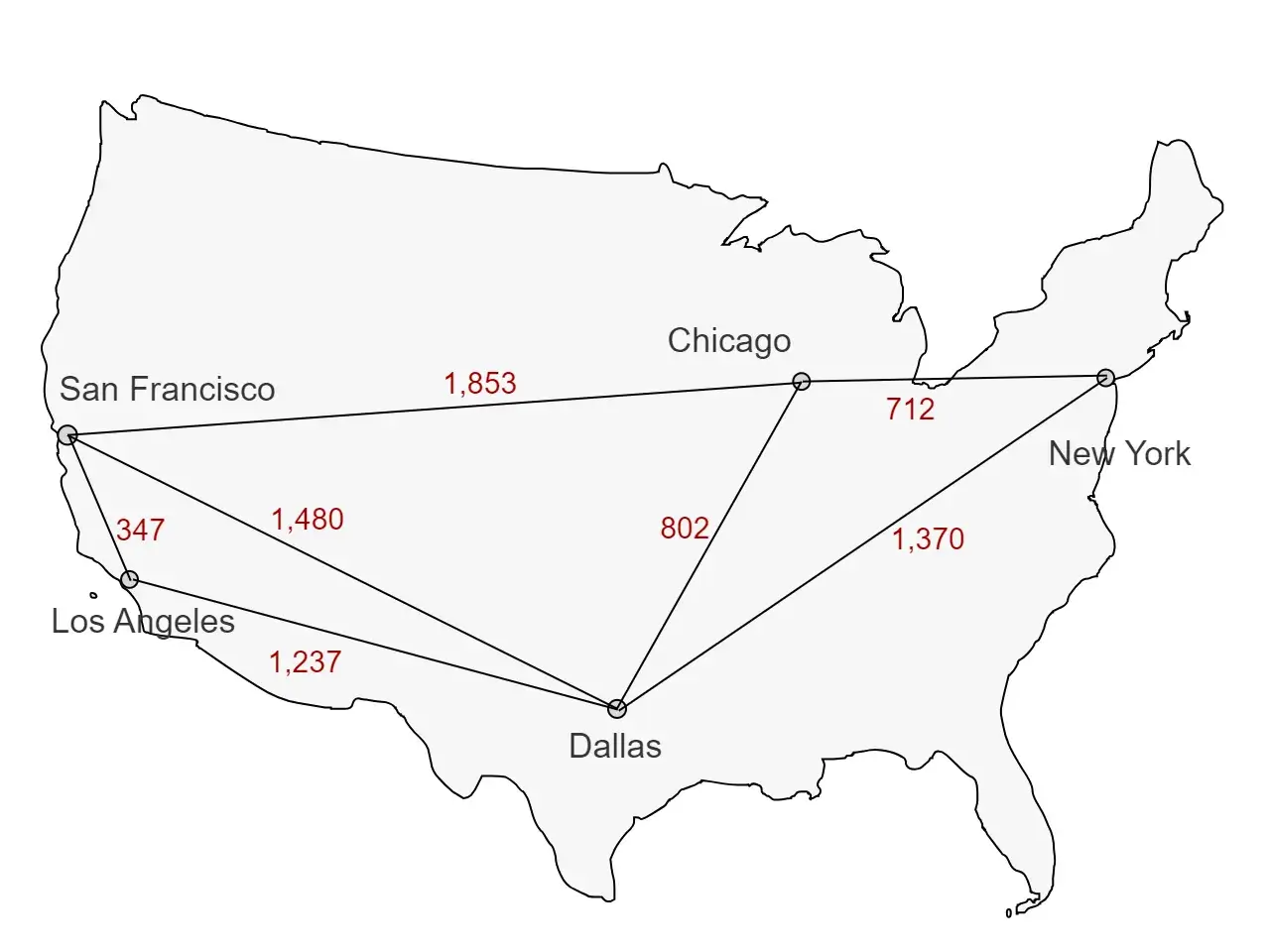
The scenario in this post is that we have some cities (the nodes of a graph) and flights that can be taken between these cities (the edges of the graph). The goal is to create a function that can find the shortest route between any two cities in the graph.
In the following sections we'll start by defining some basic types, building the graph, implementing the algorithm, and finally running the algorithm for an example.
Defining the graph
First of all, we'll define the elements of our graph: City (the nodes) and Edge (the edges). We'll also define Distance as an alias of int, just to make it easier to follow the algorithm later.
using Distance = int;
// Each City has multiple edges
public record City(string Name)
{
public Edge[] Edges { get; set; } = [];
}
// An edge has a distance, and is connected to another City
public record Edge(City ConnectedTo, Distance Distance);
With these types defined we can use them to define the create the US cities graph shown above.
// Define the cities (which are nodes)
var sanFran = new City("San Francisco");
var la = new City("Los Angeles");
var dallas = new City("Dallas");
var newYork = new City("New York");
var chicago = new City("Chicago");
// Update the cities with the distance to each connected node
sanFran.Edges = [
new Edge(la, 347),
new Edge(dallas, 1_480),
new Edge(chicago, 1_853),
];
la.Edges = [
new Edge(dallas, 1_237),
new Edge(sanFran, 347),
];
dallas.Edges = [
new Edge(chicago, 802),
new Edge(newYork, 1_370),
new Edge(sanFran, 1_480),
new Edge(la, 1_237),
];
chicago.Edges = [
new Edge(newYork, 712),
new Edge(sanFran, 1_853),
new Edge(dallas, 802),
];
newYork.Edges = [
new Edge(dallas, 1_370),
new Edge(chicago, 712),
];
// The full collection of cities
City[] allCities = [sanFran, la, dallas, newYork, chicago];
The cities and edges above match the graph previously defined, but we could easily change this definition to evaluate other networks.
I added the
Edges directly to theCitynodes in this post for convenience, but you could easily modify the code in this post to handle cases where they're defined separately, in two distinct arrays for example.
With the graph above defined, we can now implement Dijkstra's algorithm itself.
Calculating the shortest path using a priority queue
The following method, CalculateShortestPath, takes a City[], which defines the graph, and the start and end City of the path. It then returns the list of City on the shortest path (and the accumulated distance along the path). I'll first explain the high-level operation of the code, then show the annotated code, and finally walk through an example.
The overall approach is to maintain a dictionary, distances, where each City is the key and the value is the current shortest distance to that node from the start node, along with the previous node that connects as a tuple (City Previous, Distance int). By building up this dictionary, the shortest distance can be found by walking back from the final node via the Previous values.
Starting from the start node, the distance to all connected nodes is found, and is used to update the distances dictionary. Each connected node is then added to a priority queue, with a priority set to the calculated distance to the node.
In the next step, the smallest priority node is popped from the priority queue. The process then repeats: the distance from the start node, via the selected node is calculated for each of the connected nodes. If the calculated cumulative distance to each connected node is shorter than the current value for the node in the distances dictionary then the dictionary is updated, and the node is added to the queue.
This process continues until either the priority queue is empty, or until the final node is popped from the queue.
static List<(City, Distance)>? CalculateShortestPath(City[] cities, City startNode, City endNode)
{
// Initialize all the distances to max, and the "previous" city to null
var distances = cities
.Select((city, i) => (city, details: (Previous: (City?)null, Distance: int.MaxValue)))
.ToDictionary(x => x.city, x => x.details);
// priority queue for tracking shortest distance from the start node to each other node
var queue = new PriorityQueue<City, Distance>();
// initialize the start node at a distance of 0
distances[startNode] = (null, 0);
// add the start node to the queue for processing
queue.Enqueue(startNode, 0);
// as long as we have a node to process, keep looping
while (queue.Count > 0)
{
// remove the node with the current smallest distance from the start node
var current = queue.Dequeue();
// if this is the node we want, then we're finished
// as we must already have the shortest route!
if (current == endNode)
{
// build the route by tracking back through previous
return BuildRoute(distances, endNode);
}
// add the node to the "visited" list
var currentNodeDistance = distances[current].Distance;
foreach (var edge in current.Edges)
{
// get the current shortest distance to the connected node
Distance distance = distances[edge.ConnectedTo].Distance;
// calculate the new cumulative distance to the edge
Distance newDistance = currentNodeDistance + edge.Distance;
// if the new distance is shorter, then it represents a new
// shortest-path to the connected edge
if (newDistance < distance)
{
// update the shortest distance to the connection
// and record the "current" node as the shortest
// route to get there
distances[edge.ConnectedTo] = (current, newDistance);
// if the node is already in the queue, first remove it
queue.Remove(edge.ConnectedTo, out _, out _);
// now add the node with the new distance
queue.Enqueue(edge.ConnectedTo, newDistance);
}
}
}
// if we don't have anything left, then we've processed everything,
// but didn't find the node we want
return null;
}
If you find this a little hard to follow, don't worry, we'll walk through it step by step shortly.
Reconstructing the final path
Once the final node is popped, we can rebuild the shortest path description by walking back through the previous links in the distances dictionary, starting from the endNode:
static List<(City, Distance)> BuildRoute(
Dictionary<City, (City? previous, Distance Distance)> distances,
City endNode)
{
var route = new List<(City, Distance)>();
City? prev = endNode;
// Keep examining the previous version until we
// get back to the start node
while (prev is not null)
{
var current = prev;
(prev, var distance) = distances[current];
route.Add((current, distance));
}
// reverse the route
route.Reverse();
return route;
}
The final list contains each node on the shortest path, and the cumulative distance to each node. As a final bit of tidying up, we can print the shortest path to the console:
static void PrintShortestPath(City[] graph, City startNode, City endNode)
{
var route = CalculateShortestPath(graph, startNode, endNode);
if (route is null)
{
// This won't happen in our sample graph, but in general for a graph
// you can't guarantee there's always going to be a path between two nodes
Console.WriteLine($"No route could be found between {startNode.Name} and {endNode.Name}");
return;
}
Console.WriteLine($"Shortest route between {startNode.Name} and {endNode.Name}");
foreach (var (node, distance) in route)
{
Console.WriteLine($"{node.Name}: {distance}");
}
}
And we can finally run our sample using:
PrintShortestPath(allCities, startNode: sanFran, endNode: newYork);
Before we finish, we'll walk through this sample case to see how it all works.
Tracing an example execution
In the final part of this post we'll trace through the execution of the CalculateShortestPath() method (the main Dijkstra algorithm execution), calculating the shortest path between the sanFran and newYork nodes.
As the above example shows, if you execute the CalculateShortestPath() method you'll find the following shortest path is calculated:
Shortest route between San Francisco and New York
San Francisco: 0
Chicago: 1853
New York: 2565
And with that we're done looking at Dijkstra's algorithm and the .NET PriorityQueue!
Summary
In this post I described why the method Remove() was added to the PriorityQueue type in .NET 9 (preview 1): The main reason was to make it possible to use PriorityQueue to implement Dijkstra's algorithm. In the second half of the post I showed an example of how you could implement this, based on finding the shortest path between two cities, given a small graph of connected edges.