I've been listening to a lot of Sean Carroll's Mindscape podcast recently, and in a recent episode with Rob Reid he discussed the Everettian or "many-worlds" approach to explaining the measurement problem in quantum mechanics.
Towards the end of the episode they discussed an iPhone app that uses a quantum device connected to an HTTP API to "split the universe" by triggering a quantum measurement. Whether you believe the many-worlds theory or not, there's something very cool about having a quantum device just an HTTP call away… So I threw together an HttpClient to call the HTTP API to generate truly random numbers.
And voila: you have a quantum random generator! And as an added bonus, you've split the universe multiple times to get it. The focus of this post isn't the HttpClient itself - that's a toy to scratch an itch more than anything else. Instead, I'm trying to put down my (exceedingly-basic) understanding of the quantum measurement problem, and the many-worlds approach.
This is obviously a departure from my usual posts. I've always been casually interested in physics but I'm absolutely not a physicist, so I strongly suggest taking everything I say with a pinch of salt and imprecision! It's also a very brief consideration of the subject matter - I've added some podcast references at the end of the post from where I gleaned most of my understanding in this area!
Quantum mechanics and the wave equation
So what is quantum mechanics?
Quantum mechanics is the single most successful theory we have to explain the world. There's no evidence from experimental physics that suggests there's a flaw in its description of the way the world works. It seems to be the way nature works.
At its heart is the wave equation that describes the "quantum state" of the system. In classic Newtonian mechanics, the "state" of a system (e.g. a particle) is its location and its velocity - if you know those two properties, then you can completely determine the behaviour of the system by following Newton's laws. The wave equation is the quantum state, and it evolves according to the Schrödinger equation.
You can think of the wave equation as a cloud of possibilities. As Sean puts it:
The wave function you should think of as a sort of a machine. You ask it a question, “Where is the electron?” For example. And it will say, “With a certain probability you will find the following answers to your question.” If all you care about is the position of one electron, then the wave function at every point in space has a value, and that value tells you the probability of seeing the electron there.
One of the big questions is: what actually is the wave function? Is it describing a behaviour we observe, or is it something more fundamental?
One of the biggest shifts for me was understanding that electrons aren't little balls. You can't think of it as a little ball that has a 90% chance to be in one place, and a 10% chance in the other place. That implies that the ball is always somewhere we just don't know where. The answer is that it's not really a ball. It's a weird wave thing that's everywhere at once (with varying possibilities).
But how can that be so? We have huge amounts of technology that rely on our ability to manipulate electrons and other particles just as though they are little balls. How can both descriptions be correct?
That brings us to the measurement problem.
The measurement problem in quantum mechanics
The wave equation isn't just a fancy way of thinking about probabilities – the implication is that the electron actually is in both places at once. It's in a "superposition" of all the possible states. But it's never possible for us to "see" an electron in that superposition state. When you measure or observe the electron, you only ever see it in a single place. You only ever see it as a particle.
It seems then, that the act of looking at an electron causes it to behave differently, it "collapses the wave function". It's like a game of musical statues - everything is different (people are moving / the electron is behaving like a wave) until you look at it, and suddenly everyone acts casual (people freeze / the electron behaves like a particle).

One of the big problems with this is it makes an "observer" a first-class citizen in physics. But what are the requirements to be an observer? Does it have to be a person? Is a camera an observer? What about a cat, or an amoeba? It's weird…
The question of how (of if) the wave function collapses when you measure a quantum system is termed the measurement problem. There are a number of different approaches that attempt to address this problem, for example:
- The Copenhagen interpretation which appears to say "it doesn't matter, the math works, stop complaining and do some real work" 🤷♂️.
- Bohmian mechanics suggests the wave function is only part of the solution - there's extra hidden variables we don't know about.
- Dynamical collapse theories suggest that wave function collapse happens spontaneously, but that the collapse of a single particle initiates the collapse of the entire measurement apparatus.
- Hugh Everett's many-worlds interpretation suggests the wave function never collapses, rather that the universe "splits in two" - one in which the electron is in position A, one in which the electron is in position B.
This many-worlds approach is the one favoured by Sean Carroll, and is the one of interest here.
The many-worlds approach by Everett
The many-worlds approach is in many ways the most mind-bending option. Don't be surprised if your gut reaction is that it's prosperous mumbo-jumbo! I'll try and explain as I best I understand it.
The many-worlds approach suggests that when you see the wave function appear to collapse (due to an observation) it is actually the universe "splitting" into two branches. One in which the electron was in position A and one in which it was in position B.
So what is an observation in the many-worlds approach? Everett said that the universe splits when a system becomes entangled with its environment (it decoheres). Any interaction between two systems will cause decoherance, and hence will cause the universe to split.
But seeing as we're part of this universe, we (and our measuring equipment) are inherently quantum too! So any interaction we have with fundamental particles will inevitably be a quantum interaction, and the universe splits in two. In this universe, you observe the electron in position A for example, but in the other branch of the universe you observe it in position B. So in summary an "observation" is any time you cause a quantum interaction Or to use the famous Schrödinger's cat thought experiment, in one universe the cat is alive, in the other it's asleep (no cats are harmed in my thought experiments).

I haven't succeeded in getting my head fully around this yet. Both of the universes are "here" in some sense. The theory is not suggesting the universes are spatially distant (as in some multiverse theories), or that they're "wrapped up" in some higher dimensions (as in string theory). They're in the same "place" but evolving separately, and can't contact each other. Technically, they're two different vectors in Hilbert space, but that doesn't mean a lot to me conceptually!
There's a lot more to the theory that is way beyond my capabilities, but the interesting notion is that every time you have a quantum interaction, you branch the wave function and the universe "splits in two".
This is the principle that the Universe Splitter iPhone app relies on.
Splitting the universe with a quantum measurement
The Universe Splitter app is essentially a front-end to a "Quantis" brand quantum device made by ID Quantique. This device sends a photon towards a semi-reflective mirror, so that 50% of the time the photon passes through the mirror, and 50% of the time it is reflected.
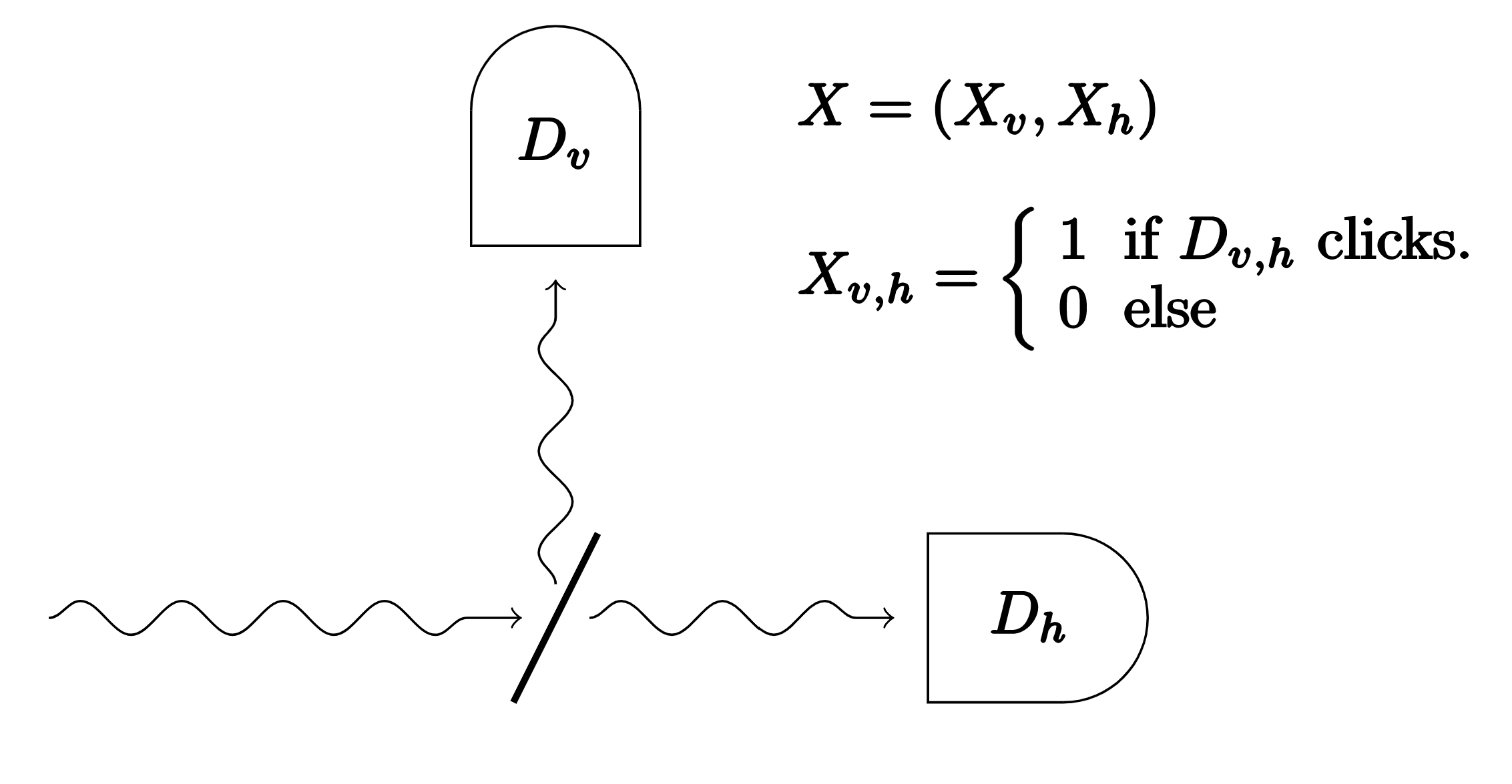
Since this is a quantum observation, then every time the device fires the universe splits in two – one branch in which the photon was reflected, and one in which it passed through! That's the premise of the Universe Splitter app. If you commit to doing action A if the photon is reflected, and action B if it transmits, then you have created two separate universes: one in which you did action A, and one in which you did action B!
This is quite a cute concept, but quantum randomness has a "real life" use too. It is the best (and only) source of true randomness. Radioactive decay is another source of randomness that can be traced back to the same quantum origin.
So I got thinking - why don't we have a quantum random generator in .NET? Sure, you can purchase a quantum random generator, and communicate with it over USB etc. But I want a web service! After a bit of hunting, I found (what I assume) is the back-end the universe splitter app is using - an API provided by ETH Zürich.
Creating a quantum random generator for .NET
The "quantum random numbers as a service, QRNGaaS" allows you to call a very simple rest API and obtain random numbers generated using a Quantis random number generator.
The API is very simple - you send a GET request, and you get back random numbers. For example, you can request 10 numbers between 0 and 9 (inclusive)
curl http://random.openqu.org/api/randint?size=10&min=0&max=9
And you'll get JSON similar to the following
{
"result":
[ 1, 3, 9, 8, 0, 4, 3, 6, 6, 3, 1]
}
There's also an API for returning floating point numbers, and base64 encoded bytes. Unfortunately, I couldn't get the bytes API to work (500 Internal Server Error).
Creating a .NET API to call this endpoint is pretty trivial. The code below is very much thrown together - it doesn't have any error checking, it creates its own HttpClient instead of having one injected via the constructor, it assumes the content will always be the expected format etc. But it works!
using System;
using System.Linq;
using System.Net.Http;
using System.Text.Json;
using System.Threading.Tasks;
public class QuantumRandomNumberGenerator
{
private readonly HttpClient _httpClient;
public QuantumRandomNumberGenerator()
{
_httpClient = new HttpClient
{
BaseAddress = new Uri("http://random.openqu.org/api/")
};
}
public async Task<int[]> GetIntegers(int min, int max, int size)
{
var url = $"randint?size={size}&min={min}&max={max}";
var stream = await _httpClient.GetStreamAsync(url);
using(var document = await JsonDocument.ParseAsync(stream))
{
return document
.RootElement
.GetProperty("result")
.EnumerateArray()
.Select(x => x.GetInt32())
.ToArray();
}
}
}
This example uses the new System.Text.Json library in .NET Core 3.0 to efficiently parse the JSON response and return the array of integers. If you want to learn more about System.Text.Json I suggest reading the intro blog post. I also liked Stuart Lang's introduction.
With our new QuantumRandomNumberGenerator defined, we can now generate truly random numbers:
var qrng = new QuantumRandomNumberGenerator();
var values = await qrng.GetIntegers(0, 255, 10);
Console.WriteLine(string.Join(", ", values));
// 32, 133, 183, 249, 208, 112, 76, 178, 44, 184
So, should you replace all your calls to RandomNumberGenerator with your shiny new QuantumRandomNumberGenerator. No, please don't. You really don't need true randomness in most places + the cost of calling an HTTP API for every new random number is clearly an issue. Add in the fact that it's a free service, no doubt exposed as a curiosity rather than providing any sorts of guarantees. Plus the fact you can only call the API over HTTP, not HTTPS. So please, don't put this into production. 😉
But do have fun thinking about all those universes you're creating. In one of them, the random list of numbers I generated above is all 0s, and in another, they're all 255s! 🤯
Resources
- Sean Carroll's Mindscape podcast. This post is based almost entirely on Sean's discussions in his podcast. In particular:
- 24 | Kip Thorne on Gravitational Waves, Time Travel, and Interstellar
- 28 | Roger Penrose on Spacetime, Consciousness, and the Universe
- 31 | Brian Greene on the Multiverse, Inflation, and the String Theory Landscape
- 36 | David Albert on Quantum Measurement and the Problems with Many-Worlds
- 45 | Leonard Susskind on Quantum Information, Quantum Gravity, and Holography
- 55 | A Conversation with Rob Reid on Quantum Mechanics and Many Worlds
- 59 | Adam Becker on the Curious History of Quantum Mechanics
- 63 | Solo: Finding Gravity Within Quantum Mechanics
- Daniel and Jorge Explain the Universe is another podcast I enjoy. It's very approachable and is a great introduction if you're not really into physics in general. In particular the following podcast finally gave me an inuitive grasp of the double slit experiment: